Para saber mais sobre geometria, lendo, clique aqui (bons slides)!
Quer entender vendo figuras? Só olhar abaixo.
As classificações comuns de lápis vão de 6b (sendo esse mácio) até 9h (h vem de "hard" do inglês" e significa duro. O nível médio de traçado e sujeira é o hb. O ideal para o desenho técnico é o lápis com grafite mais dura.


Quanto as lapiseiras, a mais indicada é a de grafite 0,5mm.

A borracha não deve deixar marcas no papel e não deve ser lavada.



No principio dos desenhos gregos (mais investigativos sobre o que sempre acontecia e sobre o que só acontecia às vezes) eles usavam réguas sem medidas marcas (cratões duros que serviam para ajudar a traçar retas).

O transferidor é uma régua que mede ângulos em graus.
Falando dos desenhos mesmo

Ponto. Nomes: letra maiúscula do nosso alfabeto.
Encontro entre linhas, não tem medidas.


Linha. Nomes: letras minusculas do nosso alfabeto.
Pode ser um ponto em movimento ou a união de infinitos pontos. Pode ser reta (possui uma única direção), curva (está em constante e suave mudança de direção), poligonal (tem mudanças bruscas de direção, pode ser vista como a união de vários pedaços de reta) ou mista (junta a forma reta e a curva).
As linhas mais usadas nos nossos estudos são as retas.


Plano. Nomes: letras gregas minúsculas
Infinito para todos os lados, contém infinitos pontos.

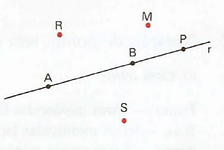






Assumimos que as retas são infinitas (linhas abertas). Isso faz das semirretas um tipo de reta com início ou fim.

Retas concorrentes
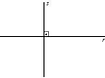
As perpendiculares separam o plano em 4 regiões iguais.

Ângulos são figuras formadas por duas semi-retas de mesma origem. Podemos dizer que na região interna a um ângulo temos um semi plano e, na região externa, outro semi-plano. Seu nome pode ser a união de três pontos que o determinam, sendo que o ponto do vértice (ponto de origem das semi-retas) leva um acento circunflexo. Podem ser, também, utilizadas as letras que dão nome para as semi-retas.

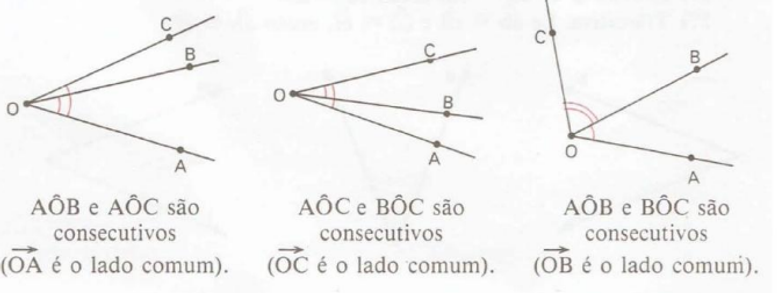

Esses ângulos são adjacentes, estão um ao lado do outro, mas não tem pontos interno comuns. O Lado OB está separando os dois.
Ângulos determinados pelas mesmas retas que ficam de frente um para o outro.

Os ângulos AÔB e BÔC são suplementares porque juntos formam a reta AC.
Por um ponto passam infinitas retas. Essas infinitas retas determinam, entre elas, infinitos ângulos. Então, os matemáticos definiram que o grau é uma divisão de uma circunferência completa em 360. Isso significa que uma volta completa tem 360º, meia volta, ou um ângulo raso, tem 180º. O ângulo reto, tem 90º graus. O ângulo reto, é o ângulo que tem como suplementar um ângulo congruente.


Agora que sabemos que o ângulo reto, o de 90º, tem como suplementar outro ângulo reto, podemos dizer que as retas que se cruzam e dividem o plano em 4 regiões congruentes são, essas retas, perpendiculares.

Os outros ângulos, maiores que o reto, são o raso, o de volta inteira e os côncavos (entre o raso e a volta inteira.
Segmentos de reta são pedaços finitos de reta, limitados por dois pontos.

E, as retas podem se cruzar, como já vimos, ou não se cruzarem nunca, como é o caso das retas paralelas

Com as figuras que você conhece agora, dá para criar outras, como



Com a ideia dos triângulos semelhantes e dos triângulos congruentes (vou deixar para próxima aula) encontramos outras particularidades sobre as figuras anteriores.
O ponto médio de um segmento, a reta bissetriz de um ângulo e as medianas e mediatriz de um segmento.



Os triângulos tem os vértices, os ângulos internos e os lados. A soma dos ângulos internos é 180º e a soma de dois lados é sempre maior que o terceiro lado.
Juntando dois triângulos, obtemos um quadrilátero.
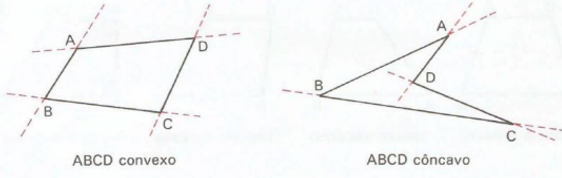


Cada quadrilátero tem sua particularidade. Não vou abordar agora porque essa aula é só apresentar a geometria. Depois de triângulos temos os polígonos, figuras com vários lados. As mais faladas são os pentágonos, os hexágonos e os octógonos. Para conhecimento do básico, até aqui está bem.
Nenhum comentário:
Postar um comentário