Fração

 Soma

https://docs.google.com/forms/d/e/1FAIpQLScYjAJme3rmTildYSrs5eF-ZcXy9pd3HrzQ71kJ_wDwW26S0w/viewform?usp=sf_link

E vamo de geometria...

3ª aula Sobre segmentos: https://docs.google.com/forms/d/e/1FAIpQLSc8sxaVLbgBuRYoGS4r3IgaE2kSa_1x8eaiBPbzMeEOwR4Jtg/viewform?usp=sf_link

2ª aula Sobre retas, linhas e planos: https://docs.google.com/forms/d/e/1FAIpQLScq1v_CFwn0ElvCxPNQTTqWDUARdrojMBfdmeyaqP2PANb4CA/viewform?usp=sf_link

1ª aula Sobre desenhar: https://docs.google.com/forms/d/e/1FAIpQLSc_dOmHhfg45R0sL60l9iq3GIit0Zhfk4shkI6I6mX50tbxvg/viewform?usp=sf_link

Quero que vocês conheçam mais a si mesmos

 Para isso, criei esse questionário de arquétipos... Ainda vou fazer sobre traços de personalidade e tipo de aprendizado:

Arquétipos: https://docs.google.com/forms/d/e/1FAIpQLSfdNWqq9yoPVP9a0wXKuYykJ12jKATKQGWvt1Ip2LWePs3CYQ/viewform?usp=sf_link

Saiba mais sobre arquétipos:

https://sebrae.com.br/sites/PortalSebrae/artigos/descubra-qual-e-o-arquetipo-da-sua-marca,ba3994229de13810VgnVCM100000d701210aRCRD

A taxa de natalidade do mundo está diminuindo e isso é um problema!

Eu esbarrei numa polêmica, nas redes sociais, que discutia a questão de não deixar para tentar engravidar só quando a vida estivesse estável. 

Dessa polêmica, saiu a reflexão desse vídeo que gravei hoje. Sempre oriento minhas alunas, menores de 15 anos, a não namorar até os 18 (😜😅😅😅😅). Mantenho o conselho, visto o tanto de problema que acontece com adolescentes.

Mas, não pensem que filhos são um problema a vida toda. Ter um filho na adolescência é MUITO, MUITO, MUITO difícil, mas crianças não são problemas. O ser humano não é um problema, apenas sua chegada merece ser planejada. E, para planejar a chegada de alguém nas nossas vidas, precisamos estar prontos. Por isso, planejem ter filhos para BEM, BEM, BEM depois da adolescência. 

"Mas prof, e se eu não quiser?" Está tudo bem! Ninguém pode te obrigar a gerar uma vida, antes dela começar a ser gerada. Apenas, não desincentive quem deseja com as ideias de que é muito difícil e/ou a ilusão de que "é melhor ter financeiro bem estável" primeiro. 

Por que ilusão? Porque não existe planejamento capaz de dar conta de desastres. Já ouvi falar de N situações que as pessoas planejaram casamento, chegada do bebê e etc. e um dos dois faleceu, logo após a chegada da criança. Ou, um dos dois planejou toda a vinda do bebê e depois descobriu que o outro o traia... Nenhum planejamento dá conta de desastres.

A vida é feita de imprevisões. Por isso o estudo e o conhecimento são mais importantes que o dinheiro, porque o conhecimento não se perde em um desastre e ainda te ajuda a controlar os hormônios na hora da dor e da raiva. O dinheiro pode ir embora num lance de azar da vida, o conhecimento te ajuda a conseguir mais.

E, nesses lances de azar da vida, está a doença na velhice. Aí a necessidade que nasçam mais seres humanos bem educados. Com mais gente nova e bem educada nascendo, mais pessoas poderão cuidar da gente na velhice e na doença. Quem já nasceu, de agora em diante, só envelhece. Se não vier pessoas para renovar e repor quem está indo, teremos um mundo envelhecido, necessitando de atenção e cuidados e não teremos.

Pra finalizar, recapitulando:

• Não tenham filhos na adolescência;
• Não deixe para ter filhos muito depois dos 36;
• Não se iludam atrás de vida estável;
• Não se iludam que o que falta é riqueza. O que falta, é sempre, conhecimento;
• Se pessoas novas não nascerem, as que já existem sofreram por falta de cuidados na velhice! 

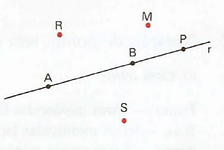
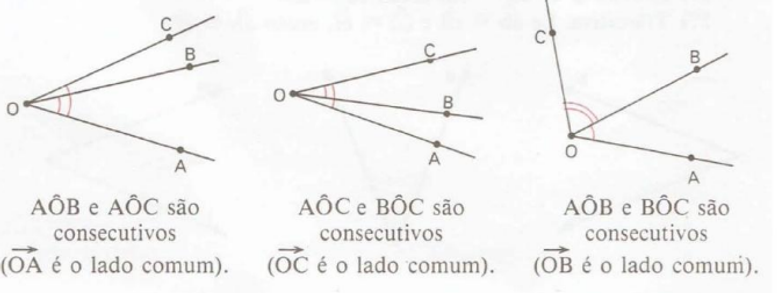
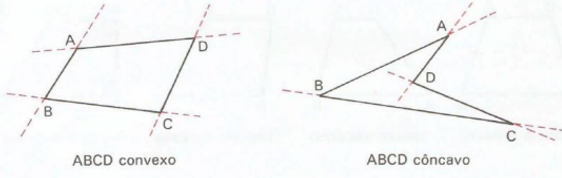
Aula de geometria para o sexto ano

 Para saber mais sobre geometria, lendo, clique aqui (bons slides)!

Quer vídeos explicando sobre geometria? Aqui!!!

Apostilas e livros que usamos em aula? aqui! (Livro difícil)

Quer entender vendo figuras? Só olhar abaixo.

As classificações comuns de lápis vão de 6b (sendo esse mácio) até 9h (h vem de "hard" do inglês" e significa duro. O nível médio de traçado e sujeira é o hb. O ideal para o desenho técnico é o lápis com grafite mais dura.

Quanto as lapiseiras, a mais indicada é a de grafite 0,5mm.

A borracha não deve deixar marcas no papel e não deve ser lavada.

No principio dos desenhos gregos (mais investigativos sobre o que sempre acontecia e sobre o que só acontecia às vezes) eles usavam réguas sem medidas marcas (cratões duros que serviam para ajudar a traçar retas).

O transferidor é uma régua que mede ângulos em graus.

Falando dos desenhos mesmo

Ponto. Nomes: letra maiúscula do nosso alfabeto.

Encontro entre linhas, não tem medidas.

Linha. Nomes: letras minusculas do nosso alfabeto.

Pode ser um ponto em movimento ou a união de infinitos pontos. Pode ser reta (possui uma única direção), curva (está em constante e suave mudança de direção), poligonal (tem mudanças bruscas de direção, pode ser vista como a união de vários pedaços de reta) ou mista (junta a forma reta e a curva).

As linhas mais usadas nos nossos estudos são as retas.

Plano. Nomes: letras gregas minúsculas

Infinito para todos os lados, contém infinitos pontos.

Assumimos que as retas são infinitas (linhas abertas). Isso faz das semirretas um tipo de reta com início ou fim.

Retas concorrentes

As perpendiculares separam o plano em 4 regiões iguais.

Ângulos são figuras formadas por duas semi-retas de mesma origem. Podemos dizer que na região interna a um ângulo temos um semi plano e, na região externa, outro semi-plano. Seu nome pode ser a união de três pontos que o determinam, sendo que o ponto do vértice (ponto de origem das semi-retas) leva um acento circunflexo. Podem ser, também, utilizadas as letras que dão nome para as semi-retas.

Esses ângulos são adjacentes, estão um ao lado do outro, mas não tem pontos interno comuns. O Lado OB está separando os dois.

Ângulos determinados pelas mesmas retas que ficam de frente um para o outro.

Os ângulos AÔB e BÔC são suplementares porque juntos formam a reta AC.

Por um ponto passam infinitas retas. Essas infinitas retas determinam, entre elas, infinitos ângulos. Então, os matemáticos definiram que o grau é uma divisão de uma circunferência completa em 360. Isso significa que uma volta completa tem 360º, meia volta, ou um ângulo raso, tem 180º. O ângulo reto, tem 90º graus. O ângulo reto, é o ângulo que tem como suplementar um ângulo congruente.

Agora que sabemos que o ângulo reto, o de 90º, tem como suplementar outro ângulo reto, podemos dizer que as retas que se cruzam e dividem o plano em 4 regiões congruentes são, essas retas, perpendiculares.

Os outros ângulos, maiores que o reto, são o raso, o de volta inteira e os côncavos (entre o raso e a volta inteira.

Segmentos de reta são pedaços finitos de reta, limitados por dois pontos.

E, as retas podem se cruzar, como já vimos, ou não se cruzarem nunca, como é o caso das retas paralelas

Com as figuras que você conhece agora, dá para criar outras, como

Com a ideia dos triângulos semelhantes e dos triângulos congruentes (vou deixar para próxima aula) encontramos outras particularidades sobre as figuras anteriores.

O ponto médio de um segmento, a reta bissetriz de um ângulo e as medianas e mediatriz de um segmento.

Os triângulos tem os vértices, os ângulos internos e os lados. A soma dos ângulos internos é 180º e a soma de dois lados é sempre maior que o terceiro lado.

Juntando dois triângulos, obtemos um quadrilátero.

Cada quadrilátero tem sua particularidade. Não vou abordar agora porque essa aula é só apresentar a geometria. Depois de triângulos temos os polígonos, figuras com vários lados. As mais faladas são os pentágonos, os hexágonos e os octógonos. Para conhecimento do básico, até aqui está bem.